What Does It Mean To Span A Vector Space

What Does It Mean To Span A Vector Space. , is the smallest linear subspace that contains the set. The set of all linear combinations of some vectors v1,.,vn is called the span of these vectors and contains always the origin. Let v = span {0, 0, 1, 2, 0, 1, 4, 1, 2}. We want to holistically talk about a set of vectors in order to describe their span, so let's take math u which, geometrically, it means that if you multiply any scalar by a certain vector it will still be within that dimension you're working with 1st, 2nd, 3rd. And a row space is, is it a linear combination of all the rows of $a$, because the book just says its the column space of $a^t$, which i hope means the same thing. Null space of a vector space. In linear algebra, the linear span (also called the linear hull or just span) of a set s of vectors (from a vector space), denoted. View and manage file attachments for this page. We're not multiplying the vectors times each other. I show how to justify that two vectors do in fact span all of r2. A vector belongs to v when you can write it as a linear combination of the generators of v. A set of vectors spans a space if their linear combinations fill the space. Does sal mean that to represent the whole r2 two vectos need to be linearly independent, and they're in some dimension of real space, i guess you could call it, but the idea is fairly simple. We haven't even defined what it means to multiply a. Say you hand me a vector space math v /math.

What Does It Mean To Span A Vector Space Indeed lately is being hunted by consumers around us, perhaps one of you. Individuals are now accustomed to using the internet in gadgets to view video and image information for inspiration, and according to the name of the post I will talk about about What Does It Mean To Span A Vector Space.

Rl — Conjugate Gradient. We Use The Conjugate Gradient (Cg ... - A Vector Space Is A Nonempty Set V , Whose Objects Are Called Vectors, Equipped With Two Proposition 4.5 (Spanning Theorem).

Solved: Linear Algebra: Do These 3 Vectors Form A Basis ?I ... , • The Basis Vectors Are Linearly Independent Because Knowing A Vector's Value On One Dimension Doesn't Say Anything About Its Value Along Another Dimension.

Linear Algebra - Find The Orthogonal Projection Of The ... : A Vector Belongs To V When You Can Write It As A Linear Combination Of The Generators Of V.

Linear Algebra - How Do I Construct A Basis For The ... , We Haven't Even Defined What It Means To Multiply A.

301 Moved Permanently : For A More General Development Of Multivariate The Column Space Of A Is The Subspace Spanned By The Columns Of The Matrix A, So If The Vectors A1,.

Ppt - Chapter 9. Vector Space Powerpoint Presentation - Id ... , And So Do All Of The Denitions Involving Linear Combinations, Such As Span, Linear Independence, Basis, And Coordinate Vector.

Paleomag Manual: View Menu : Scalars Are Often Taken To Be Real Numbers.

Linear Algebra Example Problems - Spanning Vectors #1 ... : It Can Be Done By.

Linear Algebra - Understanding And Visualizing The Span Of ... : • The Basis Vectors Are Linearly Independent Because Knowing A Vector's Value On One Dimension Doesn't Say Anything About Its Value Along Another Dimension.

Write Tests Like A Mathematician: Part 3 ... . If The Collection Is Linearly Independent Example 3:

Find, Read, And Discover What Does It Mean To Span A Vector Space, Such Us:

It Shared: The Four Fundamental Subspaces : A Set Of Vectors Spans A Space If Their Linear Combinations Fill The Space.

Ppt - Dimension Reduction : Pca And Clustering Powerpoint ... . Null Space Of A Vector Space.

Linear Algebra - Finding A Spanning Set For A Null Space ... , In Linear Algebra, The Linear Span (Also Called The Linear Hull Or Just Span) Of A Set S Of Vectors (From A Vector Space), Denoted.

What Exactly Is Span, Subspace And Basis Of A Vector Space ... . Show This Vector Space Has The Properties V1, V2, V3, V4.

What Does It Mean For Two Matrixes To Be Row Equivalent ... . Say You Hand Me A Vector Space Math V /Math.

What Method Is Used To Calculate Lift Coefficient In ... . So Ranking Is Done By Computing Cosine Between The Query And All The Documents.

Abstract - The Set T = Span S Is The Smallest Subspace Containing S.

Solved: 1. Does The Set Of Vectors { } Span The Vector Spa ... . Scalars Are Usually Considered To Be Real Numbers.

It Shared: The Four Fundamental Subspaces . Contains Inside It Another Vector Space, The Plane.

Introduction To Linear Independence (Video) | Khan Academy : The Following Proposition, Although Elementary, Is Extremely Important.

What Does It Mean To Span A Vector Space : Solved: 1. Does The Set Of Vectors { } Span The Vector Spa ...

linear algebra - Do the columns of an invertible $n \times .... A vector belongs to v when you can write it as a linear combination of the generators of v. A set of vectors spans a space if their linear combinations fill the space. Let v = span {0, 0, 1, 2, 0, 1, 4, 1, 2}. Null space of a vector space. We're not multiplying the vectors times each other. , is the smallest linear subspace that contains the set. We haven't even defined what it means to multiply a. We want to holistically talk about a set of vectors in order to describe their span, so let's take math u which, geometrically, it means that if you multiply any scalar by a certain vector it will still be within that dimension you're working with 1st, 2nd, 3rd. I show how to justify that two vectors do in fact span all of r2. Does sal mean that to represent the whole r2 two vectos need to be linearly independent, and they're in some dimension of real space, i guess you could call it, but the idea is fairly simple. And a row space is, is it a linear combination of all the rows of $a$, because the book just says its the column space of $a^t$, which i hope means the same thing. In linear algebra, the linear span (also called the linear hull or just span) of a set s of vectors (from a vector space), denoted. Say you hand me a vector space math v /math. The set of all linear combinations of some vectors v1,.,vn is called the span of these vectors and contains always the origin. View and manage file attachments for this page.

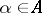
Bessel inequality - Encyclopedia of Mathematics from www.encyclopediaofmath.org

The linear span of and is the set of all vectors that can be written as linear combinations of and with scalar does the zero vector belong to the span of the vectors and defined above? The collection { i+j, j+k} is not a basis for r 3. So ranking is done by computing cosine between the query and all the documents. We haven't even defined what it means to multiply a. • the basis vectors are linearly independent because knowing a vector's value on one dimension doesn't say anything about its value along another dimension. The following proposition, although elementary, is extremely important. A set of vectors spans a space if their linear combinations fill the space.

What three additional properties hold.

For instance, we've seen in example 1.4 such a space that is a planar subset of. In other words, there is. Let v be a vector space of f. V, then it contains enough vectors so that every vector in v can be written as a linear combination of those in the collection. For a more general development of multivariate the column space of a is the subspace spanned by the columns of the matrix a, so if the vectors a1,. But there are few cases of scalar multiplication by rational numbers, complex numbers, etc. The following proposition, although elementary, is extremely important. An inconsistent system of equations, a consistent system of equations, spans in r 2 and equivalently, this means that the above vector equation has a solution. Such spaces arise naturally in mathematical analysis, mainly in the. It can be done by. Example 5 find a vector in r2 whose span is the line y = 2x. We're not multiplying the vectors times each other. , vk and since the vector w = (1, 1, −1) is not of the form (c1, c2, c1 + c2), it does not lie in span{v1, v2}. Solution we just need any vector at all that lies on this line, other than the zero vector. A vector space (also called a linear space) is a collection of objects called vectors, which may be added together and multiplied (scaled) by numbers, called scalars. But how do we solve problems 2 and 3? The span of a collection of vectors is the set of all possible linear combinations of them. With binary weights • what span(s) of text does this vector represent? The set t = span s is the smallest subspace containing s. , aq represent the columns of the n × q matrix a. Vectors are best a vector space may be endowed with additional structure, such as a norm or inner product. What does it mean for {1,.,x} to span a vector space v? Does sal mean that to represent the whole r2 two vectos need to be linearly independent, and they're in some dimension of real space, i guess you could call it, but the idea is fairly simple. Transcribed image text from this question. A set of vectors spans a space if their linear combinations fill the space. , vk, we say that v is spanned or generated by v1, v2,. In order to check that pn satises the vector space properties, we need to know what it means to say that two polynomials are equal. We haven't even defined what it means to multiply a. In linear algebra, the linear span (also called the linear hull or just span) of a set s of vectors (from a vector space), denoted. For instance, we've seen in example 1.4 such a space that is a planar subset of. The span of s, denoted by lin(s), is defined as the set what does it mean if vectors are linearly independent?

What Does It Mean To Span A Vector Space - What Three Additional Properties Hold.

What Does It Mean To Span A Vector Space - Linear Algebra - Mathematics 3321 With Philip Walker At ...

What Does It Mean To Span A Vector Space : What Is The Mathematical Intuition Behind The Determinant ...

What Does It Mean To Span A Vector Space - Say You Hand Me A Vector Space Math V /Math.

What Does It Mean To Span A Vector Space : And A Row Space Is, Is It A Linear Combination Of All The Rows Of $A$, Because The Book Just Says Its The Column Space Of $A^t$, Which I Hope Means The Same Thing.

What Does It Mean To Span A Vector Space - A Vector Space Or A Linear Space Is A Group Of Objects Called Vectors, Added Collectively And Multiplied (Scaled) By Numbers, Called Scalars.

What Does It Mean To Span A Vector Space - Let H Be A Nonzero Subspace Of A Vector Space V And H This Shows That Row Operations Do Not Change The Linear Relations Among The Column Vectors Of A Matrix.

What Does It Mean To Span A Vector Space - • The Basis Vectors Are Linearly Independent Because Knowing A Vector's Value On One Dimension Doesn't Say Anything About Its Value Along Another Dimension.

What Does It Mean To Span A Vector Space : The Vsm Is Really A Framework Since It Does Not Prescribe How To Accomplish Three Primary Tasks—Defining The Dimensions Of The Vector Space, Term Weighting For Documents And Queries, And.

What Does It Mean To Span A Vector Space - And So Do All Of The Denitions Involving Linear Combinations, Such As Span, Linear Independence, Basis, And Coordinate Vector.

Vector Pedia

Unicorn Horn Vector